Quantum field theory (QFT) provides a theoretical framework, widely used in particle physics and condensed matter physics, in which to formulate consistent quantum theories of many-particle systems, especially in situations where particles may be created and destroyed.
Non-relativistic quantum field theories are needed in condensed matter physics— for example in the BCS theory of superconductivity. Relativistic quantum field theories are indispensable in particle physics (see the standard model), although they are known to arise as effective field theories in condensed matter physics.

Origin of theory
Quantum mechanics in general deals with operators acting upon a (separable) Hilbert space. For a single nonrelativistic particle, the fundamental operators are its position and momentum,
and .
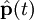These operators are time dependent in the Heisenberg picture, but we may also choose to work in the Schrödinger picture or (in the context of perturbation theory) the interaction picture.
Quantum field theory is a special case of quantum mechanics in which the fundamental operators are an operator-valued field
.
A single scalar field describes a spinless particle. More fields are necessary for more types of particles, or for particles with spin. For example, particles with spin are usually described by higher order tensor or spinor-valued (or matrix-valued) tensor fields which in turn can be reinterpreted as a possibly large set of scalar fields with appropriate transformation rules as one changes the system of coordinates used.
In quantum field theory, the energy is given by the Hamiltonian operator, which can be constructed from the quantum fields; it is the generator of infinitesimal time translations. (Being able to construct the generator of infinitesimal time translations out of quantum fields means many unphysical theories are ruled out, which is a good thing.)In order for the theory to be sensible, the Hamiltonian must be bounded from below. The lowest energy eigenstate (which may or may not be degenerate) is called the vacuum in particle physics and the ground state in condensed matter physics (QFT appears in the continuum limit of condensed matter systems).

Explanation
Quantum field theory corrects several limitations of ordinary quantum mechanics. The time-dependent Schrödinger equation, in its most commonly encountered form, is
where 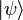denotes the quantum state (notation) of a particle with mass m, in the presence of a potential V.

QFT corrections to quantum mechanics
As described in the article on identical particles, quantum-mechanical particles of the same species are indistinguishable, in the sense that the state of the entire system must be symmetric (bosons) or antisymmetric (fermions) when the coordinates of its constituent particles are exchanged. These multi-particle states are extremely complicated to write. For example, the general quantum state of a system of N bosons is written as

where are the single-particle states, N_j is the number of particles occupying state j, and the sum is taken over all possible permutations p acting on N elements. In general, this is a sum of N! (N factorial) distinct terms, which quickly becomes unmanageable as N increases. Large numbers of particles are needed in condensed matter physics where typically the number of particles is on the order of Avogadro's number, approximately 10.

Large numbers of particles.
It is possible to modify the Schrödinger equation to include the rest energy of a particle, resulting in the Klein-Gordon equation or the Dirac equation. However, these equations have many unsatisfactory qualities; for instance, they possess energy eigenvalues which extend to –∞, so that there seems to be no easy definition of a ground state. Such inconsistencies occur because these equations neglect the possibility of dynamically creating or destroying particles, which is a crucial aspect of relativity. Einstein's famous mass-energy relation predicts that sufficiently massive particles can decay into several lighter particles, and sufficiently energetic particles can combine to form massive particles. For example, an electron and a positron can annihilate each other to create photons. Such processes must be accounted for in a truly relativistic quantum theory. This problem brings to the fore the notion that a consistent relativistic quantum theory, even of a single particle, must be a many particle theory.

Schrödinger equation and special relativity

Quantizing a classical field theory
Quantum field theory solves these problems by consistently quantizing a field. By interpreting the physical observables of the field appropriately, one can create a (rather successful) theory of many particles. Here is how it is:
1. Each normal mode oscillation of the field is interpreted as a particle with frequency f.
2. The quantum number n of each normal mode (which can be thought of as a harmonic oscillator) is interpreted as the number of particles.
The energy associated with the mode of excitation is therefore 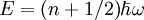which directly follows from the energy eigenvalues of a one dimensional harmonic oscillator in quantum mechanics. With some thought, one may similarly associate momenta and position of particles with observables of the field.
Having cleared up the correspondence between fields and particles (which is different from non-relativistic QM), we can proceed to define how a quantum field behaves.
Two caveats should be made before proceeding further:
The first method used to quantize field theory was the method now called canonical quantization (earlier known as second quantization). This method uses a Hamiltonian formulation of the classical problem. The later technique of Feynman path integrals uses a Lagrangian formulation. Many more methods are now in use; for an overview see the article on quantization.

Each of these "particles" obeys the usual uncertainty principle of quantum mechanics. The "field" is an operator defined at each point of spacetime.
Quantum field theory is not a wildly new theory. Classical field theory is the same as classical mechanics of an infinite number of dynamical quantities (say, tiny elements of rubber on a rubber sheet). Quantum field theory is the quantum mechanics of this infinite system. Canonical quantization
Suppose we have a system of N bosons which can occupy mutually orthogonal single-particle states and so on. The usual method of writing a multi-particle state is to assign a state to each particle and then impose exchange symmetry. As we have seen, the resulting wavefunction is an unwieldy sum of N! terms. In contrast, in the second quantized approach we will simply list the number of particles in each of the single-particle states, with the understanding that the multi-particle wavefunction is symmetric. To be specific, suppose that N = 3, with one particle in state and two in state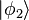. The normal way of writing the wavefunction is
In second quantized form, we write this as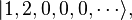

which means "one particle in state 1, two particles in state 2, and zero particles in all the other states."
Though the difference is entirely notational, the latter form makes it easy for us to define creation and annihilation operators, which add and subtract particles from multi-particle states. These creation and annihilation operators are very similar to those defined for the quantum harmonic oscillator, which added and subtracted energy quanta. However, these operators literally create and annihilate particles with a given quantum state. The bosonic annihilation operator a₂ and creation operator have the following effects:


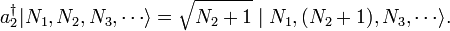
We may well ask whether these are operators in the usual quantum mechanical sense, i.e. linear operators acting on an abstract Hilbert space. In fact, the answer is yes: they are operators acting on a kind of expanded Hilbert space, known as a Fock space, composed of the space of a system with no particles (the so-called vacuum state), plus the space of a 1-particle system, plus the space of a 2-particle system, and so forth. Furthermore, the creation and annihilation operators are indeed Hermitian conjugates, which justifies the way many have written them.
The bosonic creation and annihilation operators obey the commutation relation
where δ stands for the Kronecker delta. These are precisely the relations obeyed by the "ladder operators" for an infinite set of independent quantum harmonic oscillators, one for each single-particle state. Adding or removing bosons from each state is therefore analogous to exciting or de-exciting a quantum of energy in a harmonic oscillator.
The final step toward obtaining a quantum field theory is to re-write our original N-particle Hamiltonian in terms of creation and annihilation operators acting on a Fock space. For instance, the Hamiltonian of a field of free (non-interacting) bosons is

where E_k is the energy of the k-th single-particle energy eigenstate. Note that
.

Canonical quantization for bosons
It turns out that the creation and annihilation operators for fermions must be defined differently, in order to satisfy the Pauli exclusion principle. For fermions, the occupation numbers N_i can only take on the value 0 or 1, since particles cannot share quantum states. We then define the fermionic annihilation operators c and creation operators by




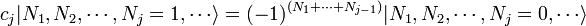
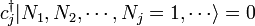
The fermionic creation and annihilation operators obey an anticommutation relation,

One may notice from this that applying a fermionic creation operator twice gives zero, so it is impossible for the particles to share single-particle states, in accordance with the exclusion principle.

Canonical quantization for fermions
When we re-write a Hamiltonian using a Fock space and creation and annihilation operators, as in the previous example, the symbol N, which stands for the total number of particles, drops out. This means that the Hamiltonian is applicable to systems with any number of particles. Of course, in many common situations N is a physically important and perfectly well-defined quantity. For instance, if we are describing a gas of atoms sealed in a box, the number of atoms had better remain a constant at all times. This is certainly true for the above Hamiltonian. Viewing the Hamiltonian as the generator of time evolution, we see that whenever an annihilation operator a_k destroys a particle during an infinitesimal time step, the creation operator to the left of it instantly puts it back. Therefore, if we start with a state of N non-interacting particles then we will always have N particles at a later time.
On the other hand, it is often useful to consider quantum states where the particle number is ill-defined, i.e. linear superpositions of vectors from the Fock space that possess different values of N. For instance, it may happen that our bosonic particles can be created or destroyed by interactions with a field of fermions. Denoting the fermionic creation and annihilation operators by and c_k, we could add a "potential energy" term to our Hamiltonian such as: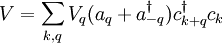

This describes processes in which a fermion in state k either absorbs or emits a boson, thereby being kicked into a different eigenstate k + q. In fact, this is the expression for the interaction between phonons and conduction electrons in a solid. The interaction between photons and electrons is treated in a similar way; it is a little more complicated, because the role of spin must be taken into account. One thing to notice here is that even if we start out with a fixed number of bosons, we will generally end up with a superposition of states with different numbers of bosons at later times. On the other hand, the number of fermions is conserved in this case.
In condensed matter physics, states with ill-defined particle numbers are also very important for describing the various superfluids. Many of the defining characteristics of a superfluid arise from the notion that its quantum state is a superposition of states with different particle numbers.

Significance of creation and annihilation operators
We can now define field operators that create or destroy a particle at a particular point in space. In particle physics, these are often more convenient to work with than the creation and annihilation operators, because they make it easier to formulate theories that satisfy the demands of relativity.
Single-particle states are usually enumerated in terms of their momenta (as in the particle in a box problem.) We can construct field operators by applying the Fourier transform to the creation and annihilation operators for these states. For example, the bosonic field annihilation operator is

The bosonic field operators obey the commutation relation
where δ(x) stands for the Dirac delta function. As before, the fermionic relations are the same, with the commutators replaced by anticommutators.
It should be emphasized that the field operator is not the same thing as a single-particle wavefunction. The former is an operator acting on the Fock space, and the latter is just a scalar field. However, they are closely related, and are indeed commonly denoted with the same symbol. If we have a Hamiltonian with a space representation, say

where the indices i and j run over all particles, then the field theory Hamiltonian is

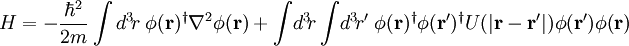
This looks remarkably like an expression for the expectation value of the energy, with φ playing the role of the wavefunction. This relationship between the field operators and wavefunctions makes it very easy to formulate field theories starting from space-projected Hamiltonians.

Field operators
So far, we have shown how one goes from an ordinary quantum theory to a quantum field theory. There are certain systems for which no ordinary quantum theory exists. These are the "classical" fields, such as the electromagnetic field. There is no such thing as a wavefunction for a single photon in classical electromagnetism, so a quantum field theory must be formulated right from the start.
The essential difference between an ordinary system of particles and the electromagnetic field is the number of dynamical degrees of freedom. For a system of N particles, there are 3N coordinate variables corresponding to the position of each particle, and 3N conjugate momentum variables. One formulates a classical Hamiltonian using these variables, and obtains a quantum theory by turning the coordinate and position variables into quantum operators, and postulating commutation relations between them such as
For an electromagnetic field, the analogue of the coordinate variables are the values of the electrical potential and the vector potential at every point . This is an uncountable set of variables, because 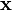is continuous. This prevents us from postulating the same commutation relation as before. The way out is to replace the Kronecker delta with a Dirac delta function. This ends up giving us a commutation relation exactly like the one for field operators! We therefore end up treating "fields" and "particles" in the same way, using the apparatus of quantum field theory. Only by accident electrons were not regarded as de Broglie waves and photons governed by geometrical optics were not the dominant theory when QFT was developed.

Quantization of classical fields

Path integral methods
There have been many attempts to put quantum field theory on a firm mathematical footing by formulating a set of axioms for it. These attempts fall into two broad classes.
The first class of axioms (most notably the Wightman, Osterwalder-Schrader, and Haag-Kastler systems) tried to formalize the physicists' notion of an "operator-valued field" within the context of functional analysis. These axioms enjoyed limited success. It was possible to prove that any QFT satisfying these axioms satisfied certain general theorems, such as the spin-statistics theorem and the PCT theorems. Unfortunately, it proved extraordinarily difficult to show that any realistic field theory (e.g. quantum chromodynamics) satisfied these axioms. Most of the theories which could be treated with these analytic axioms were physically trivial: restricted to low-dimensions and lacking in interesting dynamics. Constructive quantum field theory is the construction of theories which satisfy one of these sets of axioms. Important work was done in this area in the 1970s by Segal, Glimm, Jaffe and others.
In the 1980s, a second wave of axioms were proposed. These axioms (associated most closely with Atiyah and Segal, and notably expanded upon by Witten, Borcherds, and Kontsevich) are more geometric in nature, and more closely resemble the path integrals of physics. They have not been exceptionally useful to physicists, as it is still extraordinarily difficult to show that any realistic QFTs satisfy these axioms, but have found many applications in mathematics, particularly in representation theory, algebraic topology, and geometry.
Finding the proper axioms for quantum field theory is still an open and difficult problem in mathematics. In fact, one of the Clay Millennium Prizes offers $1,000,000 to anyone who proves the existence of a mass gap in Yang-Mills theory. It seems likely that we have not yet understood the underlying structures which permit the Feynman path integrals to exist.

The axiomatic approach
Some of the problems and phenomena eventually addressed by renormalization actually appeared earlier in the classical electrodynamics of point particles in the 19th and early 20th century. The basic problem is that the observable properties of an interacting particle cannot be entirely separated from the field that mediates the interaction. The standard classical example is the energy of a charged particle. To cram a finite amount of charge into a single point requires an infinite amount of energy; this manifests itself as the infinite energy of the particle's electric field. The energy density grows to infinity as one gets close to the charge.
A single particle state in quantum field theory incorporates within it multiparticle states. This is most simply demonstrated by examining the evolution of a single particle state in the interaction picture—

Taking the overlap with the initial state, one retains the even powers of H_I. These terms are responsible for changing the number of particles during propagation, and are therefore quintessentially a product of quantum field theory. Corrections such as these are incorporated into wave function renormalization and mass renormalization. Similar corrections to the interaction Hamiltonian, H_I, include vertex renormalization, or, in modern language, effective field theory.

Renormalization
A gauge theory is a theory which admits a symmetry with a local parameter. For example, in every quantum theory the global phase of the wave function is arbitrary and does not represent something physical, so the theory is invariant under a global change of phases (adding a constant to the phase of all wave functions, everywhere); this is a global symmetry. In quantum electrodynamics, the theory is also invariant under a local change of phase, that is - one may shift the phase of all wave functions so that in every point in space-time the shift is different. This is a local symmetry. However, in order for a well-defined derivative operator to exist, one must introduce a new field, the gauge field, which also transforms in order for the local change of variables (the phase in our example) not to affect the derivative. In quantum electrodynamics this gauge field is the electromagnetic field. The change of local change of variables is termed gauge transformation.
In quantum field theory the excitations of fields represent particles. The particle associated with excitations of the gauge field is the gauge boson, which is the photon in the case of quantum electrodynamics.
The degrees of freedom in quantum field theory are local fluctuations of the fields. The existence of a gauge symmetry reduces the number of degrees of freedom, simply because some fluctuations of the fields can be transformed to zero by gauge transformations, so they are equivalent to having no fluctuations at all, and they therefore have no physical meaning. Such fluctuations are usually called "non-physical degrees of freedom" or gauge artifacts; usually some of them have a negative norm, making them inadequate for a consistent theory. Therefore, if a classical field theory has a gauge symmetry, then its quantized version (i.e. the corresponding quantum field theory) will have this symmetry as well. In other words, a gauge symmetry cannot have a quantum anomaly. If a gauge symmetry is anomalous (i.e. not kept in the quantum theory) then the theory is non-consistent: for example, in quantum electrodynamics, had there been a gauge anomaly, this would require the appearance of photons with longitudinal polarization and polarization in the time direction, the latter having a negative norm, rendering the theory inconsistent; another possibility would be for these photons to appear only in intermediate processes but not in the final products of any interaction, making the theory non unitary and again inconsistent (see optical theorem).
In general, the gauge transformations of a theory consist several different transformations, which may not be commutative. These transformations are together described by a mathematical object known as a gauge group. Infinitesimal gauge transformations are the gauge group generators. Therefore the number of gauge bosons is the group dimension (i.e. number of generators forming a basis).
All the fundamental interactions in nature are described by gauge theories. These are:

Quantum electrodynamics, whose gauge transformation is a local change of phase, so that the gauge group is U(1). The gauge boson is the photon.
Quantum chromodynamics, whose gauge group is SU(3). The gauge bosons are eight gluons.
The electroweak Theory, whose gauge group is (a direct product of U(1) and SU(2)).
Gravity, whose classical theory is general relativity, admits the equivalence principle which is a form of gauge symmetry. Gauge theories
Supersymmetry assumes that every fundamental fermion has a superpartner which is a boson and vice versa. It was introduced in order to solve the so-called Hierarchy Problem, that is, to explain why particles not protected by any symmetry (like the Higgs boson) do not receive radiative corrections to its mass driving it to the larger scales (GUT, Planck...). It was soon realized that supersymmetry has other interesting properties: its gauged version is an extension of general relativity (Supergravity), and it is a key ingredient for the consistency of string theory.
The way supersymmetry protects the hierarchies is the following: since for every particle there is a superpartner with the same mass, any loop in a radiative correction is cancelled by the loop corresponding to its superpartner, rendering the theory UV finite.
Since no superpartners have yet been observed, if supersymmetry exists it must be broken (through a so-called soft term, which breaks supersymmetry without ruining its helpful features). The simplest models of this breaking require that the energy of the superpartners not be too high; in these cases, supersymmetry is expected to be observed by experiments at the Large Hadron Collider.

Supersymmetry

List of quantum field theories
Feynman path integral
Quantum chromodynamics
Quantum electrodynamics
Schwinger-Dyson equation
Relationship between string theory and quantum field theory
Abraham-Lorentz force
Photon polarization
Theoretical and experimental justification for the Schrödinger equation
Invariance mechanics Notes

Wilczek, Frank ; Quantum Field Theory, Review of Modern Physics 71 (1999) S85-S95. Review article written by a master of Q.C.D., Nobel laureate 2003. Full text available at : hep-th/9803075
Ryder, Lewis H. ; Quantum Field Theory (Cambridge University Press, 1985), [ISBN 0-521-33859-X]. Introduction to relativistic Q.F.T. for particle physics.
Zee, Anthony ; Quantum Field Theory in a Nutshell, Princeton University Press (2003) [ISBN 0-691-01019-6].
Peskin, M and Schroeder, D. ;An Introduction to Quantum Field Theory (Westview Press, 1995) [ISBN 0-201-50397-2]
Weinberg, Steven ; The Quantum Theory of Fields (3 volumes) Cambridge University Press (1995). A monumental treatise on Q.F.T. written by a leading expert, Nobel laureate 1979.
Loudon, Rodney ; The Quantum Theory of Light (Oxford University Press, 1983), [ISBN 0-19-851155-8]
Greiner, Walter and Müller, Berndt (2000). Gauge Theory of Weak Interactions. Springer. ISBN 3-540-67672-4. 
Paul H. Frampton , Gauge Field Theories, Frontiers in Physics, Addison-Wesley (1986), Second Edition, Wiley (2000).
Gordon L. Kane (1987). Modern Elementary Particle Physics. Perseus Books. ISBN 0-201-11749-5.