The Bohr-Einstein debates is a popular name given to what was actually a series of epistemological challenges presented by Albert Einstein against what has come to be called the standard or Copenhagen interpretation of quantum mechanics. Since Einstein's closest friend and primary interlocutor in the "school" of Copenhagen was the physicist Niels Bohr, and since it was Bohr who provided answers to most of the challenges presented by Einstein, what was actually a friendly and fruitful series of exchanges of ideas has taken on the label of a "debate".
Einstein's position with respect to quantum mechanics is significantly more subtle and open-minded than it has often been portrayed in technical manuals and popular science articles. Be that as it may, his constant and powerful criticisms of the quantum "orthodoxy" compelled the defenders of that orthodoxy to sharpen and refine their understanding of the philosophical and scientific implications of their own theory.
Einstein's natural reference point, as mentioned above, was always Niels Bohr, as the person who, more than other members of the School of Copenhagen, was animated by a particular interest for the philosophical and epistemological aspects of the theory and drew inspiration from the surprising aspects of the microscopic world in order to present daring hypotheses about reality and about knowledge, such as his idea of complementarity. These two giants of scientific thought nurtured a profound respect for each other and they were both extremely attentive to the acute and penetrating observations of the other. The debate is not only of historical interest: as we will see Einstein's attacks often provoked reactions on the part of Bohr which called into question the crucial elements of the formalization of QM and of its interpretation. This articulated process, in which many other important scientists, from Ehrenfest and Heisenberg to Born and from Schrödinger to John von Neumann, took part, brought more and more detailed attention on certain particularly problematic points of the theory.

The principle of indeterminacy applied to time and energy
At the sixth Congress of Solvay in 1930, the indeterminacy relation just discussed was Einstein's target of criticism. His idea contemplates the existence of an experimental apparatus which was subsequently designed by Bohr in such a way as to emphasize the essential elements and the key points which he would use in his response.
Einstein considers a box (called Einstein's box; see figure) containing electromagnetic radiation and a clock which controls the opening of a shutter which covers a hole made in one of the walls of the box. The shutter uncovers the hole for a time Δt which can be chosen arbitrarily. During the opening, we are to suppose that a photon, from among those inside the box, escapes through the hole. In this way a wave of limited spatial extension has been created, following the explanation given above. In order to challenge the indeterminacy relation between time and energy, it is necessary to find a way to determine with an adequate precision the energy that the photon has brought with it. At this point, Einstein turns to his celebrated relation between mass and energy of special relativity: . From this it follows that knowledge of the mass of an object provides a precise indication about its energy. The argument is therefore very simple: if one weighs the box before and after the opening of the shutter and if a certain amount of energy has escaped from the box, the box will be lighter. The variation in mass multiplied by will provide precise knowledge of the energy emitted. Moreover, the clock will indicate the precise time at which the event of the particle's emission took place. Since, in principle, the mass of the box can be determined to an arbitrary degree of accuracy, the energy emitted can be determined with a precision ΔE as accurate as one desires. Therefore, the product ΔEΔt can be rendered less than what is implied by the principle of indeterminacy.
The idea is particularly acute and the argument seemed unassailable. It's important to consider the impact of all of these exchanges on the people involved at the time. Leon Rosenfeld, a scientist who had participated in the Congress, described the event several years later:
It was a real shock for Bohr...who, at first, could not think of a solution. For the entire evening he was extremely agitated, and he continued passing from one scientist to another, seeking to persuade them that it could not be the case, that it would have been the end of physics if Einstein were right; but he couldn't come up with any way to resolve the paradox. I will never forget the image of the two antagonists as they left the club: Einstein, with his tall and commanding figure, who walked tranquilly, with a mildly ironic smile, and Bohr who trotted along beside him, full of excitement...The morning after saw the triumph of Bohr.
The "triumph of Bohr" consisted in his demonstrating, once again, that Einstein's subtle argument was not conclusive, but even more so in the way that he arrived at this conclusion by appealing precisely to one of the great ideas of Einstein: the principle of equivalence between gravitational mass and inertial mass. Bohr showed that, in order for Einstein's experiment to function, the box would have to be suspended on a spring in the middle of a gravitational field. In order to obtain a measurement of weight, a pointer would have to be attached to the box which corresponded with the index on a scale. After the release of a photon, weights could be added to the box to restore it to its original position and this would allow us to determine the weight. But in order to return the box to its original position, the box itself would have to be measured. The inevitable uncertainty of the position of the box translates into an uncertainty in the position of the pointer and of the determination of weight and therefore of energy. On the other hand, since the system is immersed in a gravitational field which varies with the position, according to the principle of equivalence the uncertainty in the position of the clock implies an uncertainty with respect to its measurement of time and therefore of the value of the interval Δt. A precise evaluation of this effect leads to the conclusion that the relation 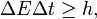, cannot be violated.

Einstein's second criticism

Main article: Hidden variable theories Second stage

Main article: Photon entanglement Third stage
In 1935 Einstein, Boris Podolsky and Nathan Rosen developed an argument, published in the magazine Physics Review with the title Is the quantum description of physical reality complete?, based on an entangled state of two particles. Before coming to this argument, it is necessary to formulate another hypothesis that comes out of Einstein's work in relativity: the idea of locality. The elements of physical reality which are objectively possessed cannot be influenced instantaneously at a distance.
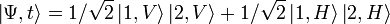
The argument of EPR can be summarized as follows:
1) Consider a system of two photons which at time t are located, respectively, in the spatially distant regions A and B and which are also in the entangled state of polarization described above:

2) At time t the photon in region A is tested for vertical polarization. Suppose that the result of the measurement is that the photon passes through the filter. According to the reduction of the wave packet, the result is that, at time t+dt, the system becomes:



3) At this point, the observer in A who carried out the first measurement on photon 1, without doing anything else that could disturb the system or the other photon, can predict with certainty that photon 2 will pass a test of vertical polarization. From assumption (R), it follows that photon 2 possesses an element of physical reality: that of having a vertical polarization.
4) According to the assumption of locality, it cannot have been the action carried out in A which created this element of reality for photon 2. Therefore, we must conclude that the photon possessed the property of being able to pass the vertical polarization test before and independently of the measurement of photon 1.
5) At time t, the observer in A could have decided to carry out a test of polarization at 45°, obtaining a certain result, for example, that the photon passes the test. In that case, he could have concluded that photon 2 turned out to be polarized at 45°. Alternatively, if the photon did not pass the test, he could have concluded that photon 2 turned out to be polarized at 135°. Combining one of these alternatives with the conclusion reached in 4, it seems that photon 2, before the measurement took place, possessed both the property of being able to pass with certainty a test of vertical polarization and the property of being able to pass with certainty a test of polarization at either 45° or 135°. These properties are incompatible according to the formalism.
6) Since natural and obvious requirements have forced the conclusion that photon 2 simultaneously possesses incompatible properties, this means that, even if it is not possible to determine these properties simultaneously and with arbitrary precision, they are nevertheless possessed objectively by the system. But quantum mechanics denies this possibility and it is therefore an incomplete theory.

The argument of EPR
Bohr's response to this fascinating and elegant argument was published, five months later than the original publication of EPR, in the same magazine Physical Review and with the exact same title as the original. The crucial point of Bohr's answer is distilled in a passage which he later had republished in Paul Arthur Schilpp's book Albert Einstein, scientist-philosopher in honor of the seventieth birthday of Einstein. Bohr attacks assumption (R) of EPR by stating:
the statement of the criterion in question is ambiguous with regard to the expression "without disturbing the system in any way". Naturally, in this case no mechanical disturbance of the system under examination can take place in the crucial stage of the process of measurement. But even in this stage there arises the essential problem of an influence on the precise conditions which define the possible types of prediction which regard the subsequent behaviour of the system...their arguments do not justify their conclusion that the quantum description turns out to be essentially incomplete...This description can be characterized as a rational use of the possibilities of an unambiguous interpretation of the process of measurement compatible with the finite and uncontrollable interaction between the object and the instrument of measurement in the context of quantum theory.
As John Bell later pointed out, this passage is almost unintelligible. What does Bohr mean, Bell asks, by the specification "mechanical" that is used to refer to the "disturbances" that Bohr maintains should not be taken into consideration? What is meant by the expression "an influence on the precise conditions" if not that different measurements in A provide different information on the system in B? This fact is not only admitted but is an essential part of the argument of EPR. Lastly, what could Bohr have meant by the expression "uncontrollable interaction between the object and the measuring apparatus", considering that the central point of the argument of EPR is the hypothesis that, if one accepts locality, only the part of the system in A can be disturbed by the process of measurement and that, notwithstanding this fact, this process provides precise information on the part of the system in B? Is Bohr already contemplating the possibility of "spooky action at a distance?" If so, why not declare it explicitly? If one abandons the assumption of locality, the argument of EPR obviously collapses immediately.
In any case, very few among the illustrious protagonists of the debate on the foundations of quantum theory were able to grasp the true sense of the profound analysis of Einstein. Pauli dismissed it with a few words and Born completely misinterpreted it. But Einstein's defeat represents one of the highest points of scientific research in the first half of the twentieth century because it called attention to an element of quantum theory, quantum non-locality, which is absolutely central to our modern understanding of the physical world.

Fourth stage

Afshar's experiment
Complementarity
Copenhagen interpretation
Double-slit experiment
EPR paradox
Quantum eraser
Schrödinger's cat
Uncertainty principle
Wheeler's delayed choice experiment